A Practical Approach to Student-Centered Instructional Practices
How can Math Milestones™ help us shift teachers’ instructional approach from one that is more teacher-centered to one that is more student-centered? How can we anchor our instruction in the 8 mathematical practices?
As a K-6 math instructional coach, I have the privilege of working with teachers at 9 different elementary sites and with all of the students who attend these sites as well. It is a daunting undertaking on some days, and on other days, it is the most rewarding experience I’ve ever been a part of.

Walking into a 5th-grade classroom, my first 5th-grade Math Milestones™ task in hand, I was eager to see all that the students would be able to show me. In professional development, we consistently talk about productive math struggle, what it looks like and what it should feel like. Now was my chance to see this in action! I printed off student copies of this first task that I would be asking them to complete, Task 5:1 Juice Box Mixup. I knew the classroom teacher had already finished teaching this concept, so this would not be anything new for the students. I briefly spoke to the students about why I was there and what I was looking for as they completed their tasks:
I’m so excited to be with all of you today. I am eager to see what you have been learning. Today I am going to ask you to complete a math task for me. It may stretch your thinking a little bit, and that is okay. I want you to take your time, consider all of the strategies that you have been learning, and show me all that you know. If you finish before others, I ask that you read the problem again and consider other solution pathways there may be.
After just a few minutes, many students seemed to be done. They had simply performed an algorithm and were not trying to solve the problem in any other way. I began to think, “Why aren’t they modeling with mathematics?” As I walked around the room, I prompted them with questions to get them to make their thinking more visible:
Can you draw a picture? What would that look like? How could you model your thinking?


Ten minutes later, all the students were done, and I collected their work. I then projected Task 5.1 Juice Box Mixup on the board and asked the students to turn to a neighbor and share their thinking. As we came back together as a class, many students asked if they could have their paper back because they had some new ideas! Students were then given 5 minutes to share their ideas as I captured their thinking on the board. When we finished, we had eight different solution pathways, students looking for and making use of structure (MP7), students critiquing the reasoning of others (MP3), and a classroom full of students (and their teacher) eager to try another task.

When I had a chance to debrief with the teacher, she quickly recognized all of the great work that she had been doing with her students. Most of the students were able to solve the problem correctly (attend to precision: MP6) and, after talking with others, many were able to reason through the problem in different ways. We marinated in that thought—that “after talking with others, many were able to reason through the problem in different ways”—for a while. What is happening during this time? Why are students better able to find different strategies when working with other students? How can this become a more regular part of math instruction? Who should be doing most of the talking, convincing, and arguing?
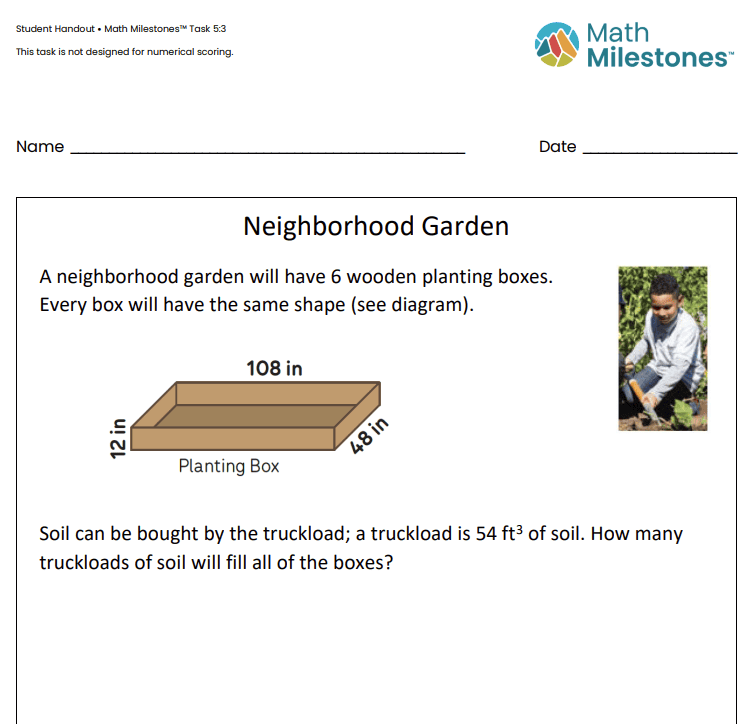
A few weeks later, I returned to the same classroom to try another task with them. This time, the classroom teacher would be leading the way. The students were eager to get started, and the teacher was excited for me to experience some of the changes she had implemented. The students were each given a student copy of Task 5:3 Neighborhood Garden. Next, the teacher asked them to take a few minutes to read the problem to themselves. They were invited to mark up the problem and add notes or ideas as they read through it (MP 7). She then used random grouping cards to place the students in groups of three, and she spaced them out around the room to work on vertical non-permanent workspaces. Students were given about 10 minutes to grapple with the problem (MP1). The teacher and I walked the room, listening to their conversations, but never interfering with their thoughts. When students were struggling, we would pose a thoughtful question to get them back on track. Some questions we found that moved student thinking forward were:
What is the problem asking you to find?
Why did you find the volume of 1 box? How will that help you? How much soil will fill 1 box?
After 10 minutes, all groups were still working. The teacher and I noticed a glaring problem: the students were all doing math well—they knew how to find the volume of 1 box and then 6 boxes. They also knew how to figure out how many of those boxes would fit in the truck; however, not one group noticed that the units of measure were different! The teacher brought all the groups back together, and she asked them to close their eyes as she read the problem to them. During that time, a few lightbulbs went off—several students remarked, “those are inches, and those are feet!” Students were sent back to work with their groups to adjust their thinking to their new learning. The next day, students were given a similar task and asked to complete it on their own. The majority of the students were able to draw on the experience from the previous day and successfully complete the task.
Students often know more than we give them credit for. Too often, the teacher gets in the way of student learning by simply doing too much. By giving a rich task like Math Milestones™, prompting students to show their thinking, allowing students to work collaboratively and only pulling them back for teacher direction to have them notice a common oversight, students were able to demonstrate their brilliance. Through these math tasks, this teacher realized the knowledge of her students, the power of working with others, and the amazing ability her students had to persevere through difficult tasks.